NUMRAT E PERJETSHEM
Numri transcendent apo i jashtezakonshem i njohur si
pi eshte thelbesor ne matematiken e avancuar. Me nje vlere paska mbi 3.14 eshte raporti i diametrit te nje rrethi me perimetrin e tij. Me fjale te tjera nese diametri i nje rrethi eshte 12 inē, perimetri i ketij rrethi do jete 12 inē x 3.14 = 37.86 inē. Gjithashtu duke qene se diametri i nje rrethi eshte saktesisht dyfishi i rrezes, ne mund te perdorim
pi per te llogaritur perimetrin e cdo rrethi nga rrezja e tij. Sidoqofte ne kete rast formula eshte gjatesia e rrezes e shumezuar me 2
pi. Le ta ilustrojme duke marre perseri nje rreth me nje diameter prej 12 inē. Rrezja e tij do jete 6 inē dhe perimetri mund te nxirret ne kete menyre: 6 inē x 2 x 3.14 = 37.68 inē. Ne menyre te ngjashme nje rreth me rreze prej 10 inē do kete nje perimeter prej 67.8 inē (10 inē x 2 x 3.14) dhe nje rreth me rreze prej 7 inē do kete nje perimeter prej 43.96 inē (7 inē x 2 x 3.14).
Keto formula qe perdorin vleren e
pi per te llogaritur perimetrin nga rrezja ose diametri, aplikohen ne te gjithe rrathet pa patur rendesi sesa te medhenj apo te vegjel jane dhe po ashtu tek te gjitha sferat dhe gjysmesferat. Ato duken relativisht te lehta nga mbrapa. Por zbulimi i tyre, i cili perfaqeson nje revolucion madheshtor ne matematike, mendohet se eshte realizuar vone ne historine e njerezimit. Kendveshtrimi ortodoks eshte qe Arkimedi ne shekullin e 3 p.e.s. ka qene njeriu i pare i cili llogariti
pi me saktesi 3.14. Studiuesit nuk e pranojne faktin qe ndonje nga matematicienet ne Boten e Re as qe mund ti jene afruar
pi perpara se te mberrinin aty europianet ne shekullin e gjashtembedhjete. Por sidoqofte eshte shume corientuese te zbulosh se Piramida e Madhe ne Giza (ndertuar me shume se 2000 vjet perpara lindjes se Arkimedit) dhe Piramida e Diellit ne Teotihuacan, e cila e predaton shume kohe me pare pushtimin spanjoll, te dyja kane te perfshira vleren e
pi. Kjo vlere eshte e nderthurur ne ate menyre qe nuk le asnje dyshim per faktin qe ndertuesit e lashte ne te dyja anet e Atlantikut kane patur njohuri per kete numer transcendental.
Faktoret kryesore te perfshire ne gjeometrine e cdo piramide jane (1) lartesia e majes nga toka dhe (2) perimetri i monumentit rrafsh me token. Persa i perket Piramides se Madhe raporti midis lartesise origjinale (481.3949 kembe) dhe perimetri (3023.16 kembe) na del te jete i njejte me raportin midis rrezes dhe perimetrit te rrethit p.sh. 2
pi. Si rezultat nese marrim lartesine e piramides dhe e shumzojme me 2
pi (sic do benim me rrezen e nje rrethi per te llogaritur perimetrin e tij) na del nje rezultat shume i sakte i perimetrit te monumentit (481.3949 kembe 2 x 3.14 = 3032.16 kembe). Ne menyre alternative nese e kthejme ekuacionin mbrapsht me perimetrin e tokes ku eshte ndertuar na del i njejti rezultat i sakte i lartesise se majes ose kulmit (3023.16 kembe pjestuar per 2 pjestuar per 3.14 = 481.3949 kembe).
Duke qene se eshte pothuajse e paimagjinueshme qe nje korrelacion matematikor kaq preciz te jete thjesht nje rastesi ne jemi te detyruar te dalim ne perfundim se ndertuesit e Piramides se Madhe kane patur njohuri te
pi dhe e kane perfshire vlerat e saj ne dimensionet e monumentit te tyre.
Tani le te marrim ne konsiderate Piramiden e Diellit ne Teotihuacan. Kendi i aneve te saj eshte 43.5° (qe i kundervihet 52° ne Piramiden e Madhe). Monumenti Meksikan ka nje pjerresi me te bute pasi perimetri i bazes se tij me 2932.8 kembe nuk eshte shume me i vogel sesa ai i nderteses ne Egjypt ndersa maja eshte ne menyre te konsiderueshme me e vogel (rreth 233.5 kembe perpara ‘restaurimit’ te Bartres).
Formula 2
pi qe funksionoi tek Piramida e Madhe nuk funksionon me keto matje. Por nje formule 4
pi funksionon. Si rezultat nese marrim lartesine e Piramides se Diellit (233.5 kembe) dhe e shumezojme me 4
pi perseri do marrim si rezultat nje shifer te sakte te perimetrit: 233.5 kembe x 4 x 3.14 = 2932.76 kembe ( nje mosperputhje fare minimale me pak se gjysem inē nga figura reale prej 2932.8 kembe).
Kjo natyrisht qe nuk mund te jete nje koincidence ashtu si dhe ne rastin e monumentin Egjyptian. Gjithashtu fakti qe te dyja strukturat permbajne mardhenien e
pi (kur asnjera nga piramidat e tjera ne te dyja anet e Atlantikut se ka) sugjeron me force jo vetem nje njohuri matematikore te avancuar ne lashtesi por edhe nje qellim thelbesor te perbashket.
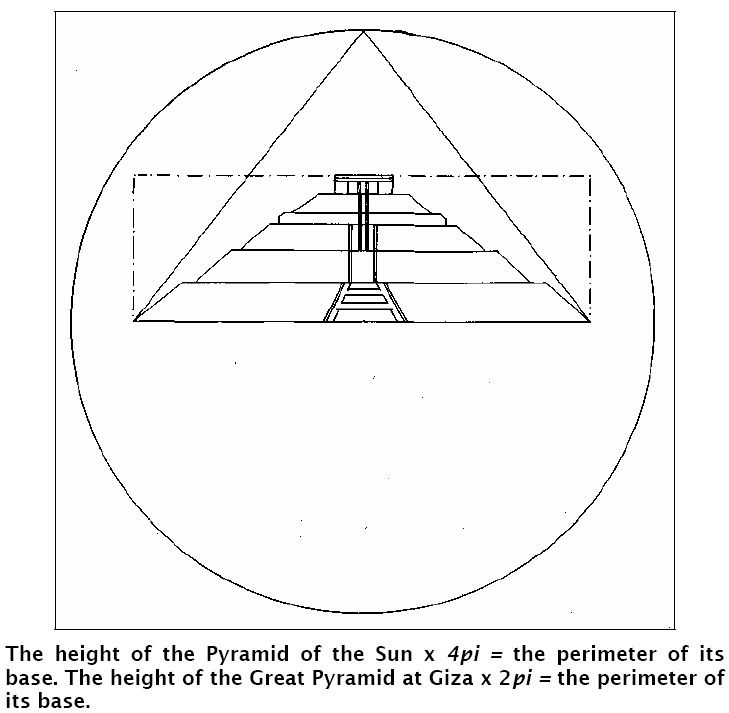
Sic e pame qe raporti i deshiruar lartesi/perimeter i Piramides se Madhe (2
pi) kerkonte nje specifikim te komplikuar dhe kend idiosinkretik te pjerresise per anet e saj: 52°. Ashtu si dhe raporti i deshiruar lartesi/perimeter i Piramides se Diellit (4
pi) kerkonte nje specifikim te nje kendi ne menyre te njejte eksentrike me pjerresine: 43.5°. Nese nuk ka patur ndonje motiv te caktuar atehere me siguri qe per Egjyptianet e Lashte dhe arkitektet Meksikane do kishte qene me e lehte per te synuar 45° (i cili do kishte qene me i lehte per tu realizuar).
Kush mund te kete qene arsyeja e perbashket qe i shtyu ndertuesit e piramidave ne te dyja anet e Atlantikut qe te perfshinin vleren e
pi me kaq precizion ne keto dy monumente madheshtore? Duke qene se (per aq sa dime) nuk ka patur kontakt direkt midis civilizimeve te Egjyptit dhe Meksikes ne periudhat kur jane ndertuar piramidat, a nuk do ishte e arsyeshme nese dilnim ne rezultatin qe keto dy kultura trasheguan kete njohuri dhe ide nga nje burim i perbashket ne kohera shume te lashta?
A eshte e mundur qe ideja e perbashket e shprehur ne Piramiden e Madhe dhe ne Piramiden e Diellit mund te kete patur lidhje me Sferen pasi keto ashtu si dhe piramidat, jane objekte tredimensionale (ndersa rrathet per shembull kane vetem dy dimensione)? Deshira per te simbolizuar sferat ne monumente tredimensionale me siperfaqe te sheshte mund te shpjegoje arsyen pse gjithe ky mundim per te perfshire mardhenien e pagabueshme te
pi. Per me shume duket i qarte qellimi i ndertuesve ne te dyja monumentet i cili nuk ishte simbolizimi i sferave ne pergjithesi por perqendrimi i vemendjes se tyre ne nje sfere te caktuar: Planeti Toke.
Do kaloje disa kohe deri sa arkeologet ortodokse do jene te pergatitur per te pranuar faktin qe disa nga njerezit e botes se lashte ishin mjaftueshem te avancuar ne shkenca per te patur ne zoterim informacione mbi formen dhe madhesine e Tokes. Sidoqofte sipas llogaritjeve te Livio Catullo Stecchini, nje profesor amerikan i Historise dhe Shkences dhe nje ekspert i mirenjohur i matjeve te lashta, evidenca per ekzistencen e nje njohurie te pazakonte ne kohen e lashte eshte e parefuzueshme. Konkluzionet e Stecchinit te cilat lidhen kryesisht me Egjyptin jane vecanerisht mbreslenese pasi ato kane dale nga te dhenat astronomike dhe matematikore te cilat jane te pranuara pertej cdo debatimi serioz. Nje analizim i metejshem i ketyre konkluzioneve dhe natyra e te dhenave ne te cilat ato bazohen paraqiten ne Pjesen e VII. Ne kete pike mbase disa fjale nga vete Stecchini mund te hedhin pak drite mbi misterin qe kemi perpara:
Ideja thelbesore e Piramides se Madhe ka qene qe ajo duhet te perfaqesonte hemisferen veriore te tokes, nje hemisfere e projektuar ne nje siperfaqe te sheshte sic behet dhe ne krjimin e hartave... Piramida e Madhe ka qene nje projeksion ne kater trekendesha siperfaqesor. Maja ose apogjeu perfaqeson polin ndersa perimetri perfaqeson ekuatorin. Kjo eshte arsyeja pse perimetri eshte ne mardhenie 2pi me lartesine. Piramida e Madhe perfaqeson hemisferen veriore ne nje shkalle 1:43.200.





 Pėrgjigju Duke Cituar
Pėrgjigju Duke Cituar




Krijoni Kontakt